Модель оптимизации инвестиционных программ с непрерывными потоками денежных платежей

Основные особенности предлагаемой модели:

· группа инвестиционных проектов формирует инвестиционную программу за счет общих финансовых ресурсов, которые должны быть распределены между отдельными проектами с учетом максимальной эффективности программы в целом;

· финансовая реализуемость инвестиционной программы достигается за счет изменения сроков начала отдельных проектов;

· каждый инвестиционный проект характеризуется динамикой денежных потоков с учетом их зависимости от времени, непрерывно изменяющегося в пределах расчетного периода.

На протяжении последних 10 лет в России ведутся интенсивные теоретические и прикладные работы в области экономического обоснования инвестиционных проектов в условиях рыночной экономики. Одним из важных результатов этих работ являются выпущенные в 1994 г. «Методические рекомендации по оценке эффективности инвестиционных проектов и их отбору для финансирования» (и их вторая редакция - в 1999 г.), утвержденные Минэкономики, Минфином и Госстроем.

Необходимо отметить, что основным направлением в работах по инвестиционному проектированию является разработка проблем эффективности отдельно взятых инвестиционных проектов. Меньшее внимание уделяется вопросам эффективности тех или иных совокупностей инвестиционных и инновационных проектов, рассматриваемых с учетом их взаимосвязей, обусловленных как достижением общих целей, так и использованием общих ресурсов. Вместе с тем, необходимость изучения проблемы экономического обоснования различного рода групп инвестиционных проектов становится все более актуальной. Эта проблема возникает в большом числе реальных и типичных ситуаций:

· при разработке целевых программ различного уровня (федеральных, региональных, отраслевых) и направленности (научно-технических, производственных, социальных, экологических, комплексных), в реализации которых принимает участие большое число хозяйствующих субъектов и органов власти;

· при подготовке инвестиционных планов холдинговых производственных структур, финансирующих взаимосвязанные инвестиционные проекты дочерних хозяйственных субъектов;

· при выработке инвестиционных стратегий финансово-промышленных групп, нацеленных на наиболее рациональное распределение финансовых потоков между входящими в них предприятиями;

· при распределении имеющихся ресурсов при подготовке ряда инвестиционных проектов на крупных предприятиях;

· при распределении средств бюджетов различных уровней для поддержки инвестиционных проектов, финансируемых из этих бюджетов;

· при отборе инвестиционных проектов для их финансирования банками.

Предпосылки построения модели

Денежные потоки инвестиционных проектов

Моделирование денежных потоков - один из основных методических приемов финансово-экономического обоснования инвестиционных проектов. Каждый инвестиционный проект характеризуется динамикой денежных потоков (притоков и оттоков). При их исследовании обычно выделяют виды деятельности и говорят о денежных потоках от инвестиционной, операционной и финансовой деятельности.

Так, инвестиции в основной и оборотный капитал представляют собой оттоки, а выручка от реализации активов - притоки денежных средств, связанные с инвестиционной деятельностью.

Выручка от реализации продукции относится к притокам денежных средств, получаемых при осуществлении операционной деятельности, а текущие затраты и налоги - к оттокам по данному виду деятельности.

В типичном случае сальдо денежных потоков проекта с учетом инвестиционной и операционной деятельности отрицательно на его начальной стадии, поскольку в этот период объем необходимых для реализации проекта капитальных вложений обычно превышает доходы от операционной деятельности, представляющие собой выручку от реализации продукции за вычетом текущих затрат и налогов. Следовательно, на начальной стадии проекта обычно возникает потребность в его финансировании.

Финансовая деятельность связана с денежными потоками, внешними по отношению к инвестиционному проекту. Поэтому к притокам относятся заемные средства, акционерный капитал, а к оттокам - погашение займов и выплата процентов, выплаты дивидендов по акциям.

Денежные потоки от финансовой деятельности необходимо учитывать при обосновании финансовой реализуемости проекта и при оценке эффективности участия в проекте.

Поскольку в работе анализируются только проблемы определения финансовой реализуемости и оценки экономической эффективности проектов и программы, нас будут интересовать не отдельные составляющие денежных потоков, а их сальдо или чистые потоки. Наряду с понятием сальдо денежных потоков используется величина накопленного сальдо денежных потоков.

Дискретные и непрерывные денежные потоки

В описании денежных потоков наиболее распространен подход, при котором их структура во времени является дискретной. Это означает, что весь расчетный период разбивается на шаги - интервалы времени. В их пределах производится агрегирование всех составляющих денежных потоков. При этом не рассматривается динамика денежных потоков внутри каждого шага и считается, что денежные потоки относятся ко всему шагу в целом.

В работе используется подход, предполагающий непрерывный характер изменения времени при описании денежных потоков. При этом необходимо оперировать интенсивностями денежных потоков. Предполагается, что известны зависимости интенсивности денежных потоков от времени, на основе которых можно построить зависимость накопленного сальдо денежных потоков от времени.

Такой подход в ряде случаев более адекватно описывает ситуации, встречающиеся при финансово-экономических обоснованиях инвестиционных проектов, чем моделирование дискретных потоков платежей. Недостатки дискретного моделирования, как правило, растут с увеличением продолжительности шагов расчета. Например, при годовых шагах расчета нивелирование динамики доходов и расходов внутри года может приводить к серьезным искажениям выводов о финансовой обеспеченности проекта.

Используя подход, основывающийся на непрерывном характере изменения времени при описании денежных потоков, предполагают, что известна функция, описывающая зависимость интенсивности сальдо денежных потоков от времени. Очень важен характер этой функции. Как правило, невозможно подобрать какую-либо аналитическую зависимость, описывающую интенсивность денежных потоков на всем расчетном периоде. Более продуктивно определять аналитические зависимости на отдельных участках расчетного периода. Поэтому будем использовать понятие этапа инвестиционного проекта, представляющего собой часть расчетного периода, на которой можно построить какую-либо аналитическую зависимость для моделирования динамики денежных потоков.

Несмотря на формальный способ определения этапа инвестиционного проекта, будем иметь в виду, что за ним, как правило, стоят объективные различия в закономерностях формирования денежных притоков и оттоков.

В целях моделирования инвестиционных проектов с непрерывными потоками платежей будем использовать понятие контрольных точек проекта, которые отделяют друг от друга последовательные этапы инвестиционного проекта. Понятно, что продолжительность этапов проекта может быть различной. Более того, у каждого инвестиционного проекта, в общем случае, имеется своя последовательность контрольных точек или временная шкала расчетов.

Наряду с понятием этапа инвестиционного проекта будем использовать понятие этапа финансирования инвестиционной программы, являющегося частью расчетного периода, на которой можно сформулировать аналитическую зависимость от времени объемов финансовых ресурсов, выделяемых программе в целом. В соответствии с этим будем говорить о контрольных точках и шкале расчетов программы.

Сроки реализации проектов

Важной предпосылкой рассматриваемой модели является возможность вариации сроков начала реализации инвестиционных проектов, входящих в инвестиционную программу. Естественно, что сдвиг начала реализации проектов возможен только в определенных пределах, поскольку значительная задержка в сроках осуществления проекта может привести к необходимости корректировки исходных данных или сделать проект неактуальным. Поэтому будем считать известными для каждого проекта максимально возможные сдвиги срока начала реализации.

Финансовая реализуемость и эффективность инвестиционной программы

Основные задачи, решаемые при финансово-экономическом обосновании инвестиционных программ, подобны задачам, возникающим при разработке отдельных инвестиционных проектов. Это, прежде всего, обеспечение финансовой реализуемости программы и оценка ее экономической эффективности. Основные подходы, используемые при решении указанных задач на уровне отдельных проектов, применимы и для обоснования инвестиционных программ. Остановимся сначала на задаче обеспечения финансовой реализуемости программы.

Под обеспечением финансовой реализуемости программы будем понимать формирование такой динамики денежных потоков, при которой на каждом шаге расчета имеется достаточное количество денежных средств для его осуществления. Критерием финансовой реализуемости программы является «неотрицательность» накопленного сальдо денежного потока на протяжении всего расчетного периода.

При оценке экономической эффективности программы будем использовать общепринятые критерии оценки абсолютной эффективности инвестиционных проектов[1]. Это означает, в первую очередь, необходимость применения такого критерия, как «положительность» чистого дисконтированного дохода (ЧДД).

ЧДД позволяет учесть разновременность затрат и результатов в течение срока жизни проекта и привести их уровень к сопоставимым условиям. Необходимым условием эффективности проекта является «положительность» ЧДД, что означает превышение приведенных результатов над приведенными затратами. Если проект будет осуществлен при отрицательном ЧДД, инвестор понесет убытки, т.е. проект для него неэффективен. Ясно, что использование ЧДД с целью получения вывода об эффективности проекта связано с предварительным определением нормы дисконта.

При определении экономической эффективности инвестиционной программы будем использовать ЧДД совокупности проектов программы в качестве оценочного показателя эффективности.

Формулировка модели

Временные шкалы и непрерывные денежные потоки проектов

Предположим, что инвестиционная программа включает в свой состав N инвестиционных проектов. Обозначим символом j индекс проекта (j = 1, 2, … , N).

Формализуем понятие временной шкалы инвестиционного проекта. Контрольные точки j-го проекта обозначим t_j,_l (j = 1, 2, … , N; l = 0, 1, 2, … , L_j). Количество контрольных точек может быть различным у разных проектов и составляет для j-го проекта величину L_j+1. Временная шкала j-го проекта представляет собой последовательность точек t_j,0, t_j,1, t_j,2, … , t_j,Lj.

Аналогично контрольные точки финансирования программы обозначим t₀,_l (l = 0, 1, 2, … , L₀), а временная шкала финансирования программы - это последовательность точек t_0,0, t_0,1, t_0,2, … , t_0,Lj.

Наконец, будем считать, что совокупность контрольных точек всех проектов и контрольные точки финансирования программы составляют вместе временную шкалу инвестиционной программы.

Заметим, что первые точки временных шкал проектов необязательно совпадают, т.е. t_j,0 не обязательно равны для всех j. Это означает, что сроки начала проектов могут отличаться друг от друга.

С учетом данного выше определения этапа инвестиционного проекта, на каждом l-ом этапе от точки t_j,l-1 до точки t_j,_l можно построить аналитическую зависимость денежных потоков от времени. Рассмотрим интенсивность сальдо денежных потоков j-го проекта как функцию времени, которую обозначим Ч_j,l (t). С помощью этой функции можно найти интенсивность сальдо денежных потоков в момент времени t, при этом будем считать, что Ч_j,l (t) определена для t, t_j,l-1 £ t < t_j,l, т.е. для определенности предположим, что в область определения функции Ч_j,l (t) входит левая граница l-го интервала и не входит его правая граница.

Если Ч_j,l (t) < 0, то в момент t интенсивность оттоков денежных средств превышает интенсивность их притоков для j-го проекта на l-ом этапе. В случае когда Ч_j,l (t) > 0, соотношение между денежными притоками и оттоками противоположное.

Предположим также, что для каждого l-го этапа программы можно построить аналитические зависимости от времени интенсивности объемов финансовых ресурсов, выделяемых программе в целом. Такие зависимости обозначим Ф_l (t).

Наряду с интенсивностью сальдо денежных потоков проекта для построения модели необходимо рассматривать накопленные величины денежных потоков в зависимости от времени, которые обозначим . Для определения зависимостей необходимо выполнить интегрирование функций на каждом l-ом этапе j-го проекта.

Аналогично введем в рассмотрение накопленные величины объемов финансовых ресурсов, выделяемых программе в целом на l-ом этапе. Такие зависимости обозначим .

Естественно предположить, что предел функции при стремлении t к t_j,l равен значению функции в точке t_j,l.

В прикладных исследованиях можно рассматривать в качестве одного из распространенных случай постоянных интенсивностей сальдо денежных потоков Ч_j,_l (t) на каждом этапе проекта. При этом накопленные величины денежных потоков представляют собой линейные функции времени. Другими словами, на всем расчетном периоде проекта интенсивность сальдо денежных потоков является кусочно-постоянной функцией времени, а накопленные величины денежных потоков - кусочно-линейной функцией.

Обозначим символом S_j - величину сдвига срока начала реализации j-го проекта. В этом случае, во-первых, произойдет соответствующая сдвижка шкал расчетов проектов, и во-вторых, зависимость от времени сальдо денежных потоков j-го проекта на l-ом этапе будет выражаться как Ч_j,_l (t – S_j). Зависимость накопленных величин денежных потоков от времени будет записываться как .

Денежные потоки инвестиционной программы

Перейдем к определению потребности в финансовых ресурсах, необходимых для реализации программы. С этой целью найдем для каждого момента времени t накопленную величину денежных потоков всей совокупности проектов, входящих в инвестиционную программу:

, (1)

где индекс k(j) выбирается для каждого j из условия t_{j,k(j) -1} £ t – S_j < t_k(j),l.

Если величина для какого-то t, то накопленная величина денежных потоков всей совокупности проектов, входящих в инвестиционную программу, в момент t не обеспечивает условие финансовой реализуемости программы и в рассматриваемый момент существует необходимость в ее внешнем финансировании. Поэтому потребность программы в финансовых ресурсах - это величина , взятая с обратным знаком, при условии что . Таким образом, потребность в финансировании трактуется как функция времени. Если же говорить о потребности в финансировании применительно ко всему расчетному периоду инвестиционной программы, то таковой является минимум функции , взятый с обратным знаком.

С учетом данного выше определения накопленной величины денежных потоков совокупности проектов, входящих в инвестиционную программу, условие финансовой реализуемости программы следует сформулировать следующим образом:

. (2)

Это ограничение (2) должно выполняться для всех t, относящихся к расчетному периоду инвестиционной программы. В этом случае инвестиционная программа обеспечена финансовыми ресурсами на протяжении всего расчетного периода и, следовательно, реализуема в финансовом отношении.

Рассмотрим упомянутый выше случай с кусочно-постоянной интенсивностью сальдо денежных потоков и, соответственно, с кусочно-линейной функцией накопленных денежных потоков. Предположим также, что кусочно-линейной от времени является функция, описывающая динамику накопленных объемов финансовых ресурсов, выделяемых программе в целом.

Пусть точки t_j,_k(j) и t_i,_k(i) принадлежат временной шкале инвестиционной программы, т.е. являются контрольными точками каких-либо проектов или контрольными точками финансирования программы. Предположим также, что эти точки являются соседними, в том смысле что между ними нет других контрольных точек инвестиционной программы. Из соседства точек t_j,_k(j) и t_i,_k(i) вытекает, что на полуинтервале [t_j,_k(j); t_i,_k(i)) для каждого проекта накопленные денежные потоки описываются какой-либо функцией . Кроме того, накопленные объемы финансовых ресурсов, выделяемых программе в целом, определяются некоторой функцией . Нетрудно заметить, что в рассматриваемом случае выполнение неравенства (2) для каких-либо соседних точек t_j,_k(j) и t_i,_k(i) влечет его выполнение для всех промежуточных точек t, t_j,_k(j) < t < t_i,_k(i).

Таким образом, в модели с кусочно-постоянными зависимостями интенсивностей сальдо денежных потоков проектов и финансирования программы условие финансовой реализуемости программы (2) следует проверять только в конечном числе точек - контрольных точках программы, включающих контрольные точки всех проектов и контрольные точки финансирования программы. Таким образом, можно записать следующие ограничения модели.

. (3)

Ограничение (3) должно выполняться для всех t_j,_l, относящихся к контрольным точкам инвестиционной программы. Неравенства (3) представляют собой ограничения, связывающие между собой переменные S_j, относящиеся к отдельным проектам.

Кроме того, переменные S_j должны удовлетворять следующим ограничениям:

0 £ S_j £ P_j , (4)

где P_j - максимальный сдвиг начала реализации j-го проекта.

В качестве целевой функции модели необходимо рассматривать ЧДД совокупности проектов. Пусть известен ЧДД каждого проекта при условии его начала в запланированные первоначально сроки. Обозначим эти величины . С учетом возможного изменения сроков начала реализации проектов и сдвига их на S_j, исходные значения необходимо корректировать на коэффициенты 1/(1+E)^Sj, где E - норма дисконта, используемая при расчете ЧДД. Таким образом, в качестве целевой функции рассматриваемой модели примем следующую величину:

. (5)

Для проведения расчетов по сформулированной модели оптимизации инвестиционных проектов предлагается использовать модуль «поиск решения» табличного процессора «Excel-2000». Серия экспериментальных расчетов показывает возможность использования этого программного средства при решении практических задач.

Пример расчетов по модели

Рассмотрим пример расчетов, выполненных с использованием описанной выше оптимизационной модели.

Инвестиционная программа включает в себя 5 инвестиционных проектов. При проведении расчетов учитывалась ограниченность финансовых ресурсов, выделяемых для реализации инвестиционной программы. Цель проведения расчетов состояла в определении оптимальных сроков начала реализации каждого проекта с учетом установленных ограничений на финансирование инвестиционной программы.

Проиллюстрируем на примере методику применения модели. В табл. 1 приведены временные шкалы инвестиционных проектов. Все они начинаются с 01.01.2002, но продолжительность отдельных этапов проектов различна. В табл. 2 приведены накопленные сальдо денежных средств за каждый этап всех проектов. На их основе рассчитываются интенсивности потоков денежных средств, показанные в табл. 3.

В табл. 4 приведено решение оптимизационной задачи и показан сдвиг в днях каждого из проектов программы. В условиях ограниченного финансирования инвестиционной программы только первый проект может быть начат в запланированные сроки. Реализация остальных проектов должна быть отложена на то или иное время. В табл. 4 показаны также контрольные точки с учетом сдвига начала реализации каждого из проектов.

Табл. 5 и 6 показывают баланс между потребностью в финансировании и имеющимися финансовыми ресурсами. Сравнение этих таблиц указывает контрольные точки, в которых ресурсы лимитируют реализацию проектов.

Алла ВЛАДИМИРОВА,

кандидат экономических наук,

доцент Государственного университета управления

Юрий РУДНЕВ,

кандидат экономических наук,

ведущий научный сотрудник Института промышленного развития

Таблица 1

Временные шкалы программы и проектов

Наименование проекта	Порядковый номер контрольной точки
	0	1	2	3	4	5	6	7	8	9
Программа	1.1.2002	1.1.2003	1.1.2004	1.1.2005	1.1.2006	1.1.2007	1.1.2008	1.1.2009	1.1.2010	1.1.2011
Проект 1	1.1.2002	1.4.2002	1.7.2002	1.10.2002	1.1.2003	1.4.2003	1.7.2003	1.10.2003	1.1.2004	1.1.2005
Проект 2	1.1.2002	1.4.2002	1.7.2002	1.10.2002	1.1.2003	1.7.2003	1.1.2004	1.1.2005	1.1.2006	1.1.2007
Проект 3	1.1.2002	1.4.2002	1.7.2002	1.10.2002	1.1.2003	1.1.2004	1.1.2005	1.1.2006	1.1.2007	1.1.2008
Проект 4	1.1.2002	1.7.2002	1.1.2003	1.7.2003	1.1.2004	1.1.2005	1.1.2006	1.1.2007	1.1.2008	1.1.2009
Проект 5	1.1.2002	1.1.2003	1.1.2004	1.1.2005	1.1.2006	1.1.2007	1.1.2008	1.1.2009	1.1.2010	1.1.2011

Таблица 2

Накопленное сальдо денежных потоков проектов на конец шага расчетов

Наименование проекта	Порядковый номер контрольной точки
	0	1	2	3	4	5	6	7	8	9
Программа
Проект 1	0,0	-2,0	-3,0	-3,0	-2,0	1,0	2,0	3,0	4,0	15,0
Проект 2	0,0	-2,0	-4,0	-4,0	-4,0	-10,0	5,0	10,0	15,0	15,0
Проект 3	0,0	-1,0	-3,0	-4,0	-4,0	8,0	10,0	12,0	12,0	12,0
Проект 4	0,0	-12,0	-10,0	-8,0	-7,0	20,0	25,0	25,0	25,0	25,0
Проект 5	0,0	-25,0	10,0	15,0	15,0	15,0	15,0	15,0	15,0	15,0

Таблица 3

Интенсивности денежных потоков проектов

Наименование проекта	Порядковый номер контрольной точки
	0	1	2	3	4	5	6	7	8	9
Программа
Проект 1	0,000	-0,022	-0,033	-0,033	-0,022	0,011	0,022	0,033	0,043	0,041
Проект 2	0,000	-0,022	-0,044	-0,043	-0,043	-0,055	0,027	0,027	0,041	0,041
Проект 3	0,000	-0,011	-0,033	-0,043	-0,043	0,022	0,027	0,033	0,033	0,033
Проект 4	0,000	-0,066	-0,054	-0,044	-0,038	0,055	0,068	0,068	0,068	0,068
Проект 5	0,000	-0,068	0,027	0,041	0,041	0,041	0,041	0,041	0,041	0,041

Таблица 4

Контрольные точки с учетом сдвига начала реализации проектов

Наименование проекта	Сдвиг, дней	Порядковый номер контрольной точки
		0	1	2	3	4	5	6	7	8	9
Программа		1.1.2002	1.1.2003	1.1.2004	1.1.2005	1.1.2006	1.1.2007	1.1.2008	1.1.2009	1.1.2010	1.1.2011
Проект 1	0	1.1.2002	1.4.2002	1.7.2002	1.10.2002	1.1.2003	1.4.2003	1.7.2003	1.10.2003	1.1.2004	1.1.2005
Проект 2	333	30.11.2002	28.2.2003	30.5.2003	30.8.2003	30.11.2003	29.5.2004	29.11.2004	30.11.2005	30.11.2006	30.11.2007
Проект 3	62	4.3.2002	2.6.2002	1.9.2002	2.12.2002	4.3.2003	3.3.2004	4.3.2005	4.3.2006	4.3.2007	3.3.2008
Проект 4	943	31.7.2004	28.1.2005	31.7.2005	28.1.2006	31.7.2006	1.8.2007	31.7.2008	31.7.2009	31.7.2010	1.8.2011
Проект 5	420	25.2.2003	25.2.2004	24.2.2005	25.2.2006	25.2.2007	25.2.2008	24.2.2009	25.2.2010	25.2.2011	25.2.2012

Таблица 5

Потребность в финансировании программы в контрольных точках проектов

Наименование проекта	Порядковый номер контрольной точки
	0	1	2	3	4	5	6	7	8	9
Проект 1	0,0	2,3	7,0	13,3	20,0	26,2	32,4	37,7	42,3	25,5
Проект 2	17,2	23,4	30,2	35,8	40,5	41,9	27,3	-3,7	-57,6	-136,3
Проект 3	1,4	5,0	11,0	17,4	23,9	45,5	21,4	-14,4	-77,5	-157,4
Проект 4	34,1	23,9	8,2	-10,3	-32,1	-109,2	-191,2	-273,1	-355,1	-437,2
Проект 5	23,0	45,7	22,0	-13,6	-76,0	-155,9	-237,8	-320,0	-401,9	-483,9

Таблица 6

Финансовые ресурсы, выделяемые программе в целом в контрольных точках проектов

Наименование проекта	Порядковый номер контрольной точки
	0	1	2	3	4	5	6	7	8	9
Проект 1	0,0	4,9	9,9	15,0	20,0	26,2	32,4	38,7	45,0	70,0
Проект 2	18,3	24,0	30,2	36,5	42,8	55,2	67,8	70,0	70,0	70,0
Проект 3	3,4	8,3	13,3	18,4	24,3	49,2	70,0	70,0	70,0	70,0
Проект 4	59,5	70,0	70,0	70,0	70,0	70,0	70,0	70,0	70,0	70,0
Проект 5	23,8	48,8	70,0	70,0	70,0	70,0	70,0	70,0	70,0	70,0

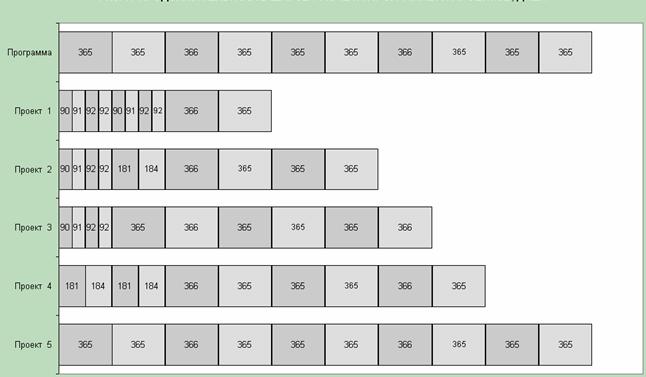
Рис. 1. Продолжительность шагов расчета программ и проектов в днях.

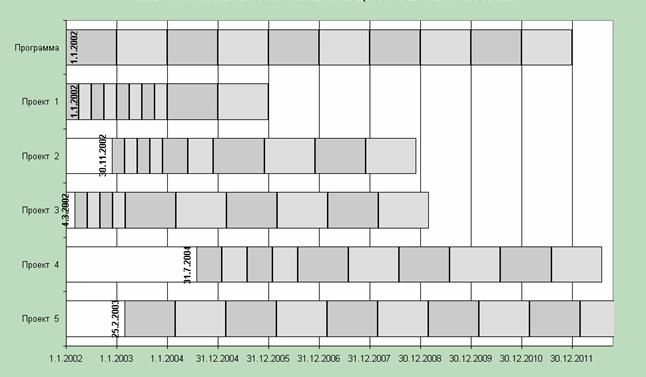
Рис. 2. Оптимальный график реализации проектов программы.

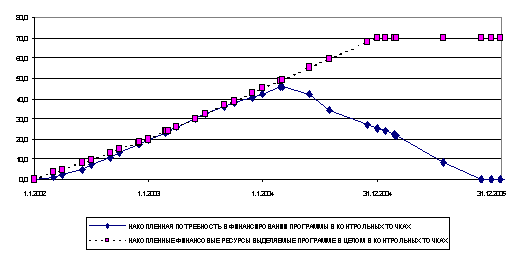
Рис. 3. Потребность в финансировании программы и имеющиеся ресурсы.

---

[1] 1. Методические рекомендации по оценке эффективности инвестиционных проектов (вторая редакция). Официальное издание. Утверждено Министерством экономики РФ, Министерством финансов РФ, Государственным комитетом по строительной, архитектурной и жилищной политике, № ВК 477 от 21.06.1999 г. (М.: Экономика, 2000).